1.3 电磁感应

一般来说，磁静场是由以匀速运动的电荷产生的，而静电场是由静止的电荷产生的。另一方面，电磁场是随时间变化的场，由时变电流产生。

这些场会根据电磁感应原理产生感应电动势（emf）。1831年，英国物理学家迈克尔·法拉第（Michael Faraday）和美国科学家约瑟夫·亨利（Joseph Henry）同时且独立地发现，线圈中磁场的任何变化都会在该线圈中感应出电动势或电压。

这种从磁场产生电动势的现象被称为电磁感应。这一原理的两个熟悉的应用是发电机（或交流发电机），它是电能的来源，以及变压器，它可以在交流电路中升高或降低电动势。

什么是电磁感应？

通过导体切割磁力线而在导体中产生感应电动势的现象或方法称为电磁感应。电动势（emf）并非如其名称所示是一种力，而是力所做的功与单位电荷的比值。它具有能量与电荷的量纲。根据法拉第的实验，这种电动势可以通过两种方式产生，即静止线圈与运动磁铁，以及静止磁铁与运动线圈。下面我们简要了解这两种方式。

静止线圈与运动磁铁

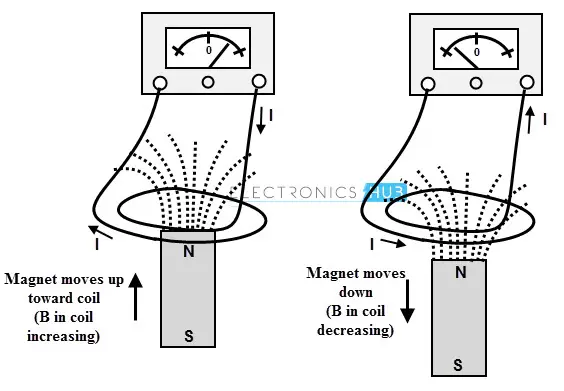
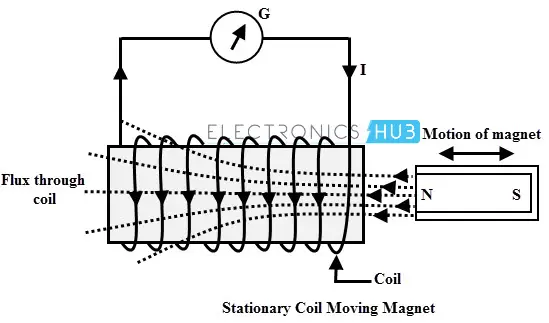
在这种方法中，保持一个有 $N$ 匝的线圈固定，而产生磁力线的永磁体相对于线圈移动。考虑下图，其中有一个 $N$ 匝的线圈连接到检流计，检流计用于指示电路中的电流。

当永磁体移动使得穿过线圈的磁力线发生变化时，检流计开始偏转。当永磁体移动得更快时，检流计的偏转也会更大。

这种电流流动的原因是由于磁力线相对于静止线圈的运动而产生的电动势。这个电动势驱动电流在电路中流动。

静止磁铁与运动线圈

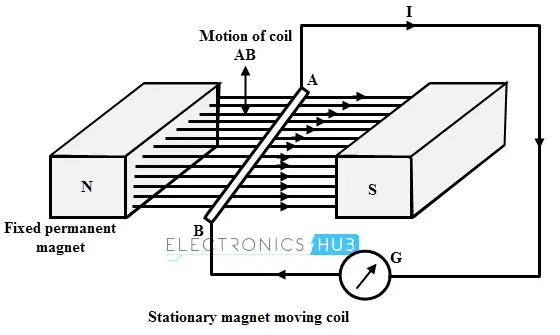
这是通过在静止磁铁产生的磁场中移动线圈来获得电动势的另一种方式。下图展示了一个装置，其中包含一个线圈 $AB$，它通过某种外部方式移动，并连接到检流计以指示电流流动。

每当 $AB$ 导体向上或向下移动时，导体就会切割磁力线。因此，在导体中感应出电动势，电流开始在电路中流动，从而检流计开始偏转。

电流的方向由导体在磁场中的运动决定。如果导体移动得更快，电流也会更大。

从上述两种方法可以看出，要产生感应电动势，必须存在磁力线相对于导体的变化。产生这种感应电动势的必要元件包括导体（或线圈）、磁场（电磁铁或永磁体）以及磁力线与导体之间的相对运动。

法拉第电磁感应定律

如上所述，两位科学家发现了电磁感应，分别是迈克尔·法拉第和约瑟夫·亨利。由于迈克尔·法拉第首先发表了这一发现，并且对电磁感应进行了更深入的研究，因此描述电磁感应的定律以他的名字命名。他提出了两条电磁感应定律。

法拉第第一定律

该定律指出，每当与闭合电路相关的磁力线（磁通量）发生变化，或者换言之，每当导体切割或被磁通量切割时，电路中就会感应出电动势，从而导致电流在电路中流动。只要磁通量发生变化或导体与磁通量之间存在相对运动，就会感应出电动势。

法拉第第二定律

该定律指出，感应电动势的大小与磁通量变化率成正比。

假设一个线圈有 $N$ 匝，初始磁通量为 $\Phi_1$。因此，与线圈相关的初始磁通量为 $N \Phi_1$。在时间 $t$ 内，与线圈相连的磁通量从 $\Phi_1$ 变化到 $\Phi_2$。那么线圈的最终磁通量为 $N \Phi_2$。

因此，磁通量变化率为

$\frac{N \Phi_2 - N \Phi_1}{t}$

根据法拉第定律，由于磁通量的变化，线圈中会产生电动势，并且根据第二定律，这个电动势与磁通量变化率成正比，即

$e \propto \frac{N \Phi_2 - N \Phi_1}{t}$ $e = \frac{N \Phi_2 - N \Phi_1}{t}$ $e = N \frac{d\Phi}{dt}$

其中 $\frac{d\Phi}{dt}$ 是磁通量的变化率，$N$ 是线圈的匝数。

根据楞次定律，这个感应电动势产生的电流方向会阻碍其产生的原因。数学上用负号表示这种阻碍，即

$e = -N \frac{d\Phi}{dt} \quad \text{(1)}$

感应电动势是一个标量量，单位为伏特。它可以用电场表示为

$e = \oint \overline{E} \cdot (d\overline{L}) \quad \text{(2)}$

上述方程表示闭合路径上的电压，如果路径的任何部分发生变化，感应的电动势也会改变。

通过特定面积的总磁通量可以用磁场表示为

$\Phi = \oint_s \overline{B} \cdot (d\overline{s})$

其中 $\overline{B}$ 是磁通密度。

那么方程 (2) 变为（假设 $N = 1$，即单匝线圈）

$e = -\frac{d}{dt} \left( \oint_s \overline{B} \cdot (d\overline{s}) \right) \quad \text{(3)}$ $\oint \overline{E} \cdot (d\overline{L}) = -\frac{d}{dt} \left( \oint_s \overline{B} \cdot (d\overline{s}) \right) \quad \text{(4)}$

这被称为楞次定律的积分形式。

考虑方程 (4) 并应用斯托克斯定理，我们得到

$\oint_s (\nabla \times \overline{E}) \cdot (d\overline{s}) = -\frac{d}{dt} \left( \oint_s \overline{B} \cdot (d\overline{s}) \right)$

如果电路是静止的，时间导数可以移到积分内部，此时它变为偏导数，即

$\oint_s (\nabla \times \overline{E}) \cdot (d\overline{s}) = -\oint_s \left( \frac{\partial}{\partial t} (\overline{B} \cdot d\overline{s}) \right)$

然后将积分相等

$\nabla \times \overline{E} = \frac{\partial}{\partial t} \overline{B}$

这被称为法拉第定律的微分形式。

楞次定律

该定律以德国物理学家海因里希·楞次（Heinrich Lenz）的名字命名，由他推导得出。该定律指出，由电磁感应产生的感应电动势的方向总是使得它产生的电流会阻碍产生它的原因。

这里的原因是磁通量的变化，它负责产生电动势。因此，感应电动势总是会阻碍产生它的原因，并且在电动势的数学表达式中用负号表示。

$e = -N \frac{d\Phi}{dt}$

考虑下图，线圈连接到一个检流计。假设一个条形磁铁向线圈移动。磁铁的移动会在线圈中感应出电动势（emf），从而产生电流。根据楞次定律，感应电流的方向会阻碍磁铁的运动，如图所示。

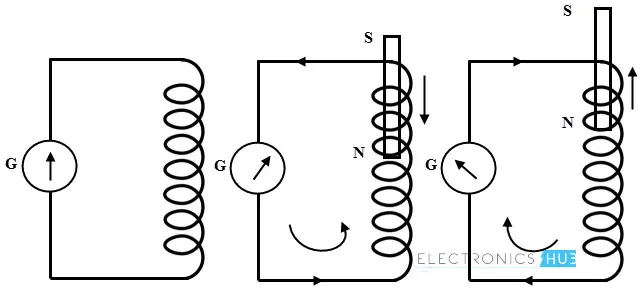
楞次定律指出，感应电流产生的磁场会阻碍产生感应电动势的磁场变化。因此，感应电流的方向总是试图抵消引起感应电动势的磁通量变化。

在下图中，由于感应电动势的作用，闭合回路中的电流呈顺时针方向流动。根据楞次定律，如果磁场 $B$ 增强，那么闭合回路中的感应电流会产生一个磁场 $B'$，以抵消通过回路的磁通量 $B$ 的增加。

那么，闭合回路中感应的电动势为：

$\oint_C \overline{E} \cdot (d\overline{l}) = -\frac{d}{dt} \left( \oint_s \overline{B} \cdot (d\overline{s}) \right)$

其中负号表示楞次定律。

电感

当线圈内部的磁场随时间变化时，线圈中产生的磁感应效应用电感 $L$ 表示。产生线圈中电动势的原因是流经线圈的电流。因此，根据楞次定律，线圈中电流的任何变化都会受到感应电动势的阻碍。

这种阻碍电流变化的特性被称为电感。线圈内部磁通量的变化不仅可能是由于线圈中电流的变化引起的，还可能是由于附近线圈中电流的变化引起的。因此，电感可以是自感或互感。

自感

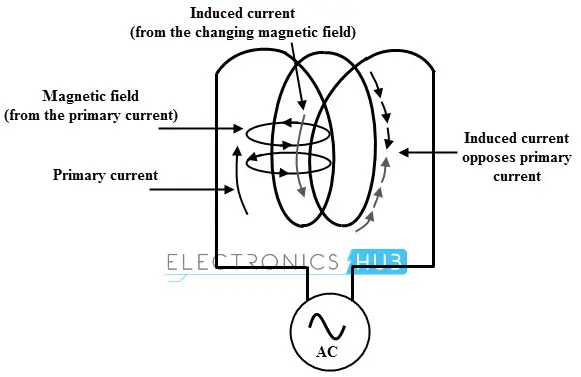
假设一个电路中有一个单匝线圈，那么电流的任何变化都会改变与电流相关的磁通量。线圈本身会截获磁通量，磁通量的变化会在线圈本身中感应出电动势。这种电动势被称为自感电动势，它驱动感应电流的方向与电流变化的方向相反。

这意味着，当电流增加时，感应电动势会减少电流，试图保持其原始值。同样，如果电流减少，感应电动势会增加电流，试图维持原始值。

因此，线圈中电流的任何变化都会受到线圈的阻碍，这种特性被称为线圈的自感。由于感应电动势阻碍了其产生的原因，这种电动势也被称为反电动势或反向电动势。

如果电路有 $N$ 个相同的匝数，那么磁通量链为 $N\Phi$。此外，如果电路周围的介质是线性的，那么磁通量链与电流成正比，即：

总磁通量链，$\lambda = N\Phi$

$\lambda \propto N\Phi$ $\lambda \propto I$ $\lambda = L I$

其中 $L$ 是一个常数，称为电感。

$L = \frac{\lambda}{I}$ $L = \frac{N\Phi}{I}$

或者

$e = -N \frac{d\Phi}{dt}$

磁通量可以表示为

$\Phi = \left( \frac{\Phi}{I} \right) \times I$

只要介质是线性的（磁导率是常数），磁通量与电流的比值就是常数。

磁通量的变化率 = $\left( \frac{\Phi}{I} \right) \times$ 电流的变化率

$\frac{d\Phi}{dt} = \left( \frac{\Phi}{I} \right) \times \frac{dI}{dt}$

代入电动势方程，我们得到

$e = -N \left( \frac{\Phi}{I} \right) \times \frac{dI}{dt}$ $e = -\left( \frac{N\Phi}{I} \right) \times \frac{dI}{dt}$

其中 $\left( \frac{N\Phi}{I} \right)$ 是自感，用 $L$ 表示。它定义为每安培电流的磁通量链，单位为亨利（H）。因此

$e = -L \frac{dI}{dt}$

进一步，自感系数可以表示为

$L = \frac{N\Phi}{I}$

但 $\Phi = \frac{\text{mmf}}{\text{磁阻}}$

$\Phi = \frac{NI}{S}$

那么

$L = \left( \frac{N}{I} \right) \times \left( \frac{NI}{S} \right)$ $L = \frac{N^2}{S}$

另外，磁阻 $S = \frac{l}{\mu a}$

其中 $l$ 是磁通路径的长度，$a$ 是磁路截面积。

那么

$L = \frac{N^2}{\left( \frac{l}{\mu a} \right)}$ $L = \frac{N^2 \mu a}{l}$ $L = \frac{N^2 \mu_0 \mu_r a}{l} \text{ 亨利}$

互感

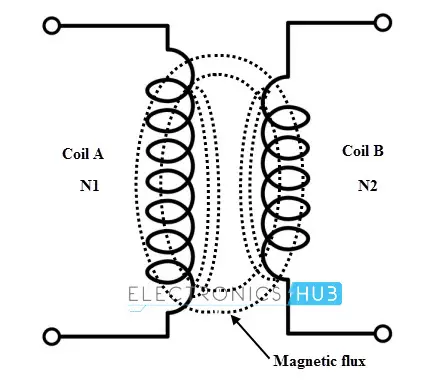
当一个电路中的电流发生变化时，在另一个相邻电路中产生感应电动势的现象称为互感。考虑两个相邻放置的线圈，如图所示。线圈 A 中的电流产生磁通量 $\Phi_1$，其中一部分磁通量与线圈 B 相连。

这部分磁通量被称为互感磁通量 $\Phi_2$。如果线圈 A 中的电流发生变化，那么磁通量 $\Phi_1$ 也会随之变化。由于这个磁通量与线圈 B 相关联，互感磁通量 $\Phi_2$ 的变化会在线圈 B 中感应出电动势。这种电动势被称为互感感应电动势。

这个电动势进一步驱动线圈 B 中的电流。因此，互感是由于另一个线圈中电流的变化而在一个线圈中感应出电动势的特性。

线圈 B 中感应的电动势为：

$e_2 = -N_2 \frac{d\Phi_2}{dt}$

负号表示根据楞次定律，感应电动势产生的电流会阻碍与线圈相连的磁通量的变化。

我们可以将 $\Phi_2$ 表示为：

$\Phi_2 = \left( \frac{\Phi_2}{I_1} \right) \times I_1$

如果介质的磁导率是常数，那么 $\Phi_2$ 与 $I_1$ 成正比，因此比值 $\left( \frac{\Phi_2}{I_1} \right)$ 是常数。

磁通量 $\Phi_2$ 的变化率为：

$\frac{d\Phi_2}{dt} = \left( \frac{\Phi_2}{I_1} \right) \times \frac{dI_1}{dt}$

因此，感应的电动势为：

$e_2 = -N_2 \left( \frac{\Phi_2}{I_1} \right) \times \frac{dI_1}{dt}$ $e_2 = -\left( \frac{N_2 \Phi_2}{I_1} \right) \times \frac{dI_1}{dt}$

在上述方程中，$\left( \frac{N_2 \Phi_2}{I_1} \right)$ 是互感，用 $M$ 表示。它定义为一个线圈中的总磁通量链与另一个线圈中每安培电流变化的比值。它的单位是亨利（H）。因此，感应的电动势为：

$e_2 = -M \times \frac{dI_1}{dt}$

进一步，互感可以表示为：

$M = \frac{N_2 \Phi_2}{I_1}$

其中 $\Phi_2$ 是由于 $I_1$ 产生的磁通量 $\Phi_1$ 的一部分。假设 $K_1$ 是与线圈 B 相连的 $\Phi_1$ 的比例，即：

$\Phi_2 = K_1 \Phi_1$

那么：

$M = \frac{N_2 K_1 \Phi_1}{I_1}$

磁通量 $\Phi_1$ 可以表示为：

$\Phi_1 = \frac{\text{mmf}}{\text{磁阻}} = \frac{N_1 I_1}{S}$

因此：

$M = \frac{N_2 K_1}{I_1} \times \frac{N_1 I_1}{S} = \frac{K_1 N_1 N_2}{S}$

如果线圈 A 产生的总磁通量与线圈 B 相连，则 $K_1 = 1$：

$M = \frac{N_1 N_2}{S}$

但 $S = \frac{l}{\mu a}$，因此：

$M = \frac{N_1 N_2}{\frac{l}{\mu a}} = \frac{N_1 N_2 \mu_0 \mu_r a}{l} \text{ 亨利}$

这是线圈 B 相对于线圈 A 的互感。从数学上讲，线圈 B 由于线圈 A 产生的互感和线圈 A 由于线圈 B 产生的互感是相同的。

螺线管的电感

考虑一个有 $N$ 匝的螺线管，如图所示。假设流经螺线管的电流为 $I$ 安培，横截面积为 $A$，螺线管的长度为 $l$。

螺线管的磁场强度为：

$H = \frac{NI}{l} \text{ 安培/米}$

总磁通量链为：

$N \Phi = N B A = N \mu H A = \mu N H A$

将 $H$ 代入上述方程：

$\text{总磁通量链} = \mu N \left( \frac{NI}{l} \right) A = \frac{\mu N^2 I A}{l}$

因此，螺线管的电感为：

$L = \frac{\text{总磁通量链}}{\text{总电流}} = \frac{\frac{\mu N^2 I A}{l}}{I} = \frac{\mu N^2 A}{l} \text{ 亨利}$

环形磁芯的电感

考虑一个半径为 $R$、有 $N$ 匝的环形磁芯，如图所示。假设流经环形磁芯的电流为 $I$ 安培。

环形磁芯内部的磁通密度为：

$B = \frac{\mu N I}{2\pi R}$

环形磁芯中 $N$ 匝的总磁通量链为：

$\text{总磁通量链} = N \Phi = N B A = N \left( \frac{\mu N I}{2\pi R} \right) A = \frac{\mu N^2 I A}{2\pi R}$

因此，环形磁芯的电感为：

$L = \frac{\text{总磁通量链}}{\text{总电流}} = \frac{\frac{\mu N^2 I A}{2\pi R}}{I} = \frac{\mu N^2 A}{2\pi R}$

其中 $A$ 是环形磁芯的横截面积，等于 $\pi r^2$ 平方米。

对于一个内半径为 $r_1$、外半径为 $r_2$、高度为 $h$、总匝数为 $N$ 的环形磁芯，其电感为：

$L = \frac{\mu N^2 h}{2\pi} \ln \left( \frac{r_2}{r_1} \right)$

电磁感应的应用实例

发电机

发电机将机械能转化为电能（与将机械能转化为电能的电动机功能相反）。

发电机的转轴通过某种机械方式（如涡轮机或发动机）旋转，从而根据法拉第电磁感应定律在绕组中感应出电动势。

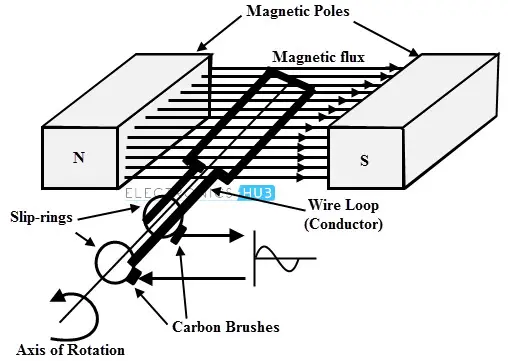
发电机的工作原理可以通过一个在均匀磁场中旋转的线圈来解释，如上图所示。但在实际发电机中，导线通常缠绕在铁芯上。

每根导线形成一个线圈，线圈的两端通过与线圈一起旋转的滑环连接到外部电路。

外部电路连接到静止的电刷上，当每个滑环滑动时，电刷与滑环接触。在发电机中，磁通量可以是运动的或静止的，这取决于导体是静止的还是运动的。

在上图中，静止的磁通量由永磁体产生，导体或线圈相对于静止的磁通量运动。由于导体和磁通量之间的相对运动，在线圈或导体中感应出电动势。

这个电动势驱动电流流向外部负载电路。当导体的运动平面与磁通量平面平行时，感应的电动势为零；当它们垂直时，感应的电动势最大。这种电动势也被称为动态感应电动势。

变压器

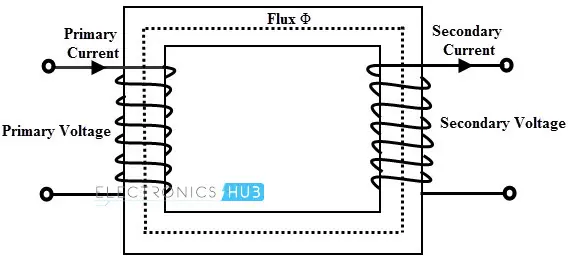
变压器本质上由一个闭合的铁芯上的两个或多个绕组组成。通过使用变压器，可以从一个交流电路将功率传输到另一个交流电路，并根据需要改变电压和电流水平。变压器基于两个线圈之间的互感原理工作。

当在初级绕组上施加电压时，电流通过它并在铁芯中建立磁通量。这个磁通量在初级线圈中感应出电动势，该电动势必须与施加的电压完全相等且方向相反。相同的磁通量也与铁芯另一端的次级绕组相连。

因此，根据电磁感应原理，次级绕组中感应出电动势。与各自绕组相关的电动势取决于每个绕组的匝数。因此，变压器在电路之间没有电气连接的情况下，将功率从一个电路传输到另一个电路。

通过适当选择次级与初级的匝数比，可以获得所需的从初级到次级的电压比。

除了这些主要的例子之外，还有许多应用利用电磁感应原理来实现其功能，例如电能传输、感应炉、工业熔炉、医疗设备、电磁流量传感器、乐器（如电小提琴和电吉他）等。